Helping ACME-ExpertSnowPlowers

As your instructor said it in class, there are many situations when you'll have to use your knowledge about graphs to solve real-life problems. The problem described here is one people in certain businesses (road-construction, communications, etc.) face all the time.

A letter to your instructor from the president of ACME-ExpertSnowPlowers is included. A complete description of the problem is included in a memo from your instructor.

What you'll turn in

1. A well commented listing of your program. Note that grading, as described below, considers both the functionality and the readability of your code. You may also want to have a look at a grading sheet used in the past for a similar assignment. If you are unsure about what the documentation of a program means, then you may want to read this document.
2. A floppy disk (3.5") which contains the source file(s) for your program, a DOS executable named acme_eps and a README file indicating what the program does, how to build the executable, the platform it's been tested on, and how to run it, plus any other information you consider useful - like the name of the author, etc. Also two input files (use the extension .din for the name), one corresponding to the problem described by the president of ACME-ExpertSnowPlowers and another one you have used to test your program, and the corresponding output files (with the extension .out).
3. A memo describing your work. You will indicate what you have looked for and how you solved the problem. Direct the memo to your class instructor. A hardcopy of the program and a paper which introduces the necessary theoretical background will be attached to the memo. Also attach a hardcopy of your sample input and the output corresponding to it.

Grading

1. A mark between 0 and 10 for functionality. The mark basically indicates in what measure your program works properly and how well you have followed the initial specification.
2. A mark between 0 and 10 for readability. This mark indicates how well documented your program is; it also considers the general appearance of your final report.
3. Multiply the above two marks to get the mark for this programming assignment.

For each business day you turn in your project earlier you receive a 5% bonus. However, penalties increase by 5% as well. You can turn in your assignment up to ten business days ahead of the deadline.
Example:

• You turn in your assignment three days earlier: a 3*5=15% bonus will be added to your assignment mark
• We find a single mistake in the functionality section and the penalty for that mistake is 0.5 points. Since you have turned the assignment three days earlier than the deadline, the penalty becomes 0.5*(1+3*5%)=0.5*(1+3*0.05)=0.575
• We calculate the mark by multiplying the marks for the functionality and readability; in your case the mark for functionality is 10-0.575=9.425, and the mark for readability is 10. The result is 9.425*10=94.25
• We add the bonus to this mark: 94.25+94.25*15%=108.38 which we round to 108. This is your final mark.

You may be asked to do a code review with your instructor.

	ACME-ExpertSnowPlowers

Chicago, 2/1/1997

Dear Virgil,

As you know, the weather forecast says that there is more snow for us in the weeks to come. This is fine with us and we really love snowy winters.

However we have a problem with a customer, a big company located in the western suburbs; they are very picky when it comes to having the snow removed from the roads that connect their buildings. Let me explain. They say that they need to have cleaned road connecting any two buildings as early as possible after the snowfall has ceased. My problem here is that I don't really know how to dispatch my plowers: to me it makes sense to have several plowers working at the same time until we meet our customer's demand, and then leave just one working until all roads are clean.

Can you help me with this? What roads should I clean first?

Thanks a lot and hope to see you soon,

Denny Roadman

P.S. What about a beer at your place (the BOG?) sometime next week?

D.R.

Attachment: A map describing our's customer buildings and roads. Buildings are represented by the red bubbles and all distances are in yards.

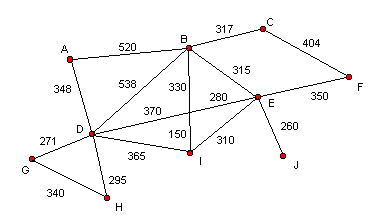
Department of Computer Science and Applied Mathematics

A business in Chicago has asked me to find a solution to their problem. I pass the problem on to you and I just add some details about input ond output formats. The problem can be modelled as a graph problem. What you have to do is to write a general program that takes a description of a connected graph from standard input, finds the shortest system of edges in the graph such that any two vertices are connected, and prints the result out to standard output.

Here is a description for the input and the output of your program.

Input

The first line in the input indicates the number of vertices in the graph. Each graph has at least two vertices. The second line in the input indicates what vertex to begin with. Each additional line in the input will give the names of two vertices and the weight of the edge connecting them. For simplicity vertex names are positive integers. Weights are integers as well. Each edge may be listed only once and your program must verify it. Here is an example of input for a graph with three vertices:

3
2
1 2 35
2 3 46

Output

The output will contain one line for each edge in the result. The output line contains the names of the vertices being connected, followed by the weight of the edge connecting them. The final line should be a sentence indicating the total weight. Here is an output line:

4    9     317

Varia

When you have your program running, solve the problem described by the president of ACME-ExpertSnowPlowers. You will assume that plowers start from the building b(your_SSN mod 10), where the function b is described by

Have fun,

Virgil

(c) 1997, Virgil Bistriceanu - virgil@csam.iit.edu
Posted: February 7, 1997
Last update: February 7, 1997